 Оценка 735
[+1/-0]
Оценка 735
[+1/-0]

 Оценить
Оценить 





 Оценка 735
[+1/-0] Оценка 735
[+1/-0]
  Оценить Оценить       
|
Целые числа сотворил Бог, а всё прочее – дело рук человеческих. Леопольд Кронекер
Зачем числам плавающие запятые? Куда они плывут? Каким стилем? Как это связано с дробями?
На все эти животрепещущие вопросы вы найдёте ответ ниже. А на какие не найдёте – те отпадут сами…
Грубо говоря (очень грубо и абстрактно), «число с плавающей запятой» это синоним для «число, записанное в экспоненциальной форме». Примерно так:
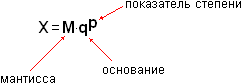
Рис. 1. Число в экспоненциальном виде
| ПРИМЕЧАНИЕ Пара слов про термины: * Мантиссу англичане называют по-разному: significand, mantissa, fraction (точнее, fraction это дробная часть – не совсем мантисса, но близко). По-русски – только мантисса. * Показатель степени по-английски будет exponent. Русских варианта три: собственно «показатель степени», порядок, экспонента. |
То, что таким образом можно записать любое число достаточно очевидно, хотя бы потому, что обычное представление это частный случай экспоненциального – когда показатель степени равен 0. Дальше, несложно заметить, что такое представление не однозначно: мы можем делить/умножать мантиссу на основание, соответственно меняя показатель степени.
1,23 *105 = 12,3 * 104 = 1230 * 102 = 0,123 * 106 = 1230000 * 10-1 |
Но о неоднозначности пока забудем, вернёмся к ней позже, а пока разберёмся, как такие числа складывать, вычитать, умножать и делить.
| ПРИМЕЧАНИЕ Поскольку нам надо всего лишь обосновать несколько несложных алгоритмов, мы не будем строить общую теорию, и просто считаем M действительным числом, q – действительным числом больше 1, а p – целым. |
Самые простые операции. Пусть:
X1 = M1qp1 X2 = M2qp2 |
Тогда:
X1 * X2 = M1qp1 * M2qp2 = M1 * M2 * qp1 * qp2 = (M1 * M2) * qp1+p2 X1 / X2 = M1qp1 / M2qp2 = M1 / M2 * qp1 / qp2 = (M1 / M2) * qp1-p2 |
То есть, при умножении нужно перемножить мантиссы и сложить показатели степени, при делении – разделить мантиссы и вычесть из показателя степени делимого показатель степени делителя. Например:
(1,2*105) * (2*10-2) = (1,2 * 2) * 105-2 =2,4*103 |
Если показатели степени равны, сложение-вычитание реализуются элементарно. Пусть:
X1 = M1qp X2 = M2qp |
Тогда:
X1 + X2 = M1qp + M2qp = (M1 + M2) * qp X1 - X2 = M1qp - M2qp = (M1 - M2) * qp |
То есть, просто выносим qp за скобку и складываем-вычитаем мантиссы. Если показатели степени отличаются, нужно воспользоваться неоднозначностью представления, и выровнять значения показателей степени. Это можно сделать многими способами, например, так:
X1 = M1qp1 X2 = M2qp2 X1 + X2 = M1qp1 + M2qp2 = (M1 + M2*qp2-p1) * qp1 |
После чего нужно привести M2*qp2-p1 к нормальному (т.е. к обычному, без показателя степени) виду, сложить с M1 результат и будет мантиссой суммы, а показателем степени суммы будет p1.
В цифрах:
1,2*105 + 2*10-2 = (1,2 + 2*10-2-5) * 105 = (1,2 + 2*10-7) * 105 = (1,2 + 0,0000002) * 105 = 1,2000002 * 105 |
In theory there is no difference between theory and practice. In practice there is. Yogi Berra
Жизнь отличается от математики наличием нескольких логичных ограничений (некоторые математические конструкции не представимы на практике) и договорённостей (в основном для удобства). Ну и следствий из них.
До сих пор нас не слишком интересовало, в каком виде записано M и чему равно q, алгоритмы сложения/умножения корректны в любом случае. Например, можно было работать с числами типа 1/3 * 7-5. Но, скажем так, это не слишком удобно. Отныне и присно:
Понятно, что при умножении/делении такого M на такое q запись результата отличается от записи M только положением запятой: если умножаем, запятая смещается вправо (1,23 * 10 = 12,3), если делим – влево (1,23 / 10 = 0,123; при необходимости, справа/слева добавляются нули). Грубо говоря, мантисса определяет, какие цифры и в каком порядке входят в число, а показатель степени – где в нём стоит запятая.
У математика в распоряжении потенциально бесконечное количество разрядов для записи мантиссы и показателя степени, на практике наши ресурсы ограничены. А при аппаратной реализации они ещё и фиксированы: регистры имеют конкретный размер, АЛУ рассчитано на работу с определённым форматом данных, всё, что в него не помещается, приходится так или иначе отбрасывать. Естественно, это приводит к потере точности и необходимости правильного округления. А иногда и к переполнениям.
Например, допустим, что мы храним три разряда мантиссы и один разряд показателя степени. Тогда:
1,23 * 104 + 3,45*10-3 = (1,23 + 0,000000345) * 104 = 1,230000345 * 104 = = (округляем до трёх значащих разрядов) = 1,23 * 104 1,23 * 104 – 3,45*10-3 = (1,23 – 0,000000345) * 104 = 1,229999655 * 104 = = (округляем до трёх значащих разрядов) = 1,23 * 104 |
К сожалению, обычно вычисляемые формулы состоят не только из арифметических действий над хорошими числами. И тут возникает ещё две проблемы:
То есть, даже если бы у нас было неограниченное количества разрядов, для точного представления значения sin(1) понадобилось бы и бесконечное количество времени: результат – иррациональное число, вычислить его «точно» невозможно, итерационный алгоритм может работать и работать, давая всё более и более верные приближения, «окончательный ответ» он не получит никогда. Правда, мы можем получить значение функции (или иррационального числа) с любой заданной точностью. Сказали четыре знака – будет четыре, сказали десять – вычислим десять, только это может оказаться значительно (на несколько порядков) дольше. Аналогично, при вычислении по таблице можно построить таблицу для любой заданной наперёд точности, вопрос только в её размере.
| ПРИМЕЧАНИЕ Обе проблемы исчезают, если решать задачи аналитически, а не численно. Например, если в процессе вычислений откуда-то появилось число π, вместо замены его на приближённое 3,14, можно честно помнить, что это именно π. Естественно, π нельзя будет просто так складывать с обычными числами, зато отлично работает функция sin(π). Но если синус так нигде и не встретится, ответ будет не числом, а формулой – некоторой функцией от π. Аналогично для любой иррациональной константы и для значений функций, которые не могут быть вычислены точно. При таком подходе в качестве результата пользователь получает формулу, а если ему всё-таки нужно число, он уже сам вычисляет его, как умеет. На этом принципе основаны системы символьной математики (Maple, Derive, Mathematica, MatLab и т.п.), обычно это большие и сложные программные пакеты. Реализовать подобный подход аппаратно… скажем так: сложно и не нужно. Хотя бы – не нужно как базовый механизм вычислений. |
Если входными данными являются не абстрактные числа, а результаты измерений физических величин, нам не поможет ни бесконечное количество разрядов, ни сколь угодно большое количество итераций алгоритмов – точность приборов ограничена. Более того, даже если мы сконструируем идеальную линейку, при попытке «точно» измерить, например, объём собственной талии, очень быстро обнаружится, что это не постоянная величина, она колеблется в некоторых пределах. Причём «гуляет» уже второй знак, так что нет смысла повышать точность даже до третьего. А с учётом того, что и идеальной линейки нет…
Корректная обработка чисел с погрешностями – большой и сложный вопрос выходящий далеко за рамки статьи. Познавательный флейм на эту тему (его можно использовать как неформальное «введение в проблематику», примерно через пару страниц диалога, наконец, появились какие-то аргументы) см., например, здесь: http://www.rsdn.ru/Forum/message/2471281.flat.1.aspx.
Число с плавающей запятой называется нормализованным, если выполняется условие:
1 <= |M| < q |
Если q это не только основание числа с плавающей запятой, но и основание системы счисления, в которой записано M (т.е. в 99% случаев), условие сводится к тому, что в мантиссе запятая стоит после первого значащего разряда.
Понятно, что в принципе, любое число кроме нуля можно записать в такой форме.
34,56 * 103 = 3,456 * 104 0,076 * 10-5 = 7,600 * 10-7 |
Понятны и плюсы – при таком расположении запятой мы никогда не храним лишних нулей, в результате в фиксированную по размеру мантиссу влезает максимум значащих разрядов. Другое дело, что нам может не хватить места для показателя степени.
567,1 * 109 = 5,671 * 1011 (потребовалось два разряда) 0,0089 * 10-8 = 8,900 * 10-11 (потребовалось два разряда) |
Согласно существующим стандартам на форматы, числа с плавающей запятой хранятся в нормализованном виде практически всегда.
| ПРИМЕЧАНИЕ Традиционное исключение – слишком маленькие по модулю числа. Например, если минимальный показатель степени -9 то, если формат позволяет, 8,900 * 10-11 будет записано как 0,089 * 10-9. Но эта ситуация рассматривается именно как исключение. |
Если множество действительных чисел это прямая, то множество чисел, представимых в виде <подставьте название любого конечного формата>, это конечное множество точек на прямой. Точки упорядочены, переход от точки к точке – прибавление/вычитание единицы к младшему разряду и (для форматов с плавающей запятой), если необходимо, нормализация.
Пример числовой прямой для формата с фиксированной запятой показан на рисунке 2, представимые числа отмечены красными точками (формат 4:1 – четыре знака перед запятой, один после).
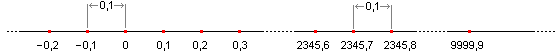
Рис. 2. Пример множества чисел, представимых в формате с фиксированной запятой
Характерный признак – постоянный шаг. Два соседних числа с фиксированной запятой всегда отличаются на одну и ту же дельту – в данном случае на 0,1. Этим они похожи на целые числа.
У чисел с плавающей запятой картина совершенно иная. На рисунке 3 кусочек числовой прямой изображён в «истинном» масштабе (формат немного игрушечный: мантисса 1 десятичный знак, показатель степени от -3 до +4).

Рис. 3. Пример множества чисел, представимых в формате с плавающей запятой, истинный масштаб
Видно, что у каждой следующей части шаг увеличивается в 10 раз, это естественное следствие увеличения показателя степени. То, что в данном случае шаг равен всем предыдущим частям вместе взятым – совпадение, если бы мантисса была длиннее, шаг был бы меньше.
На рисунке 4 менее игрушечный формат (мантисса 3 десятичных знака, показатель степени от -3 до +4, для маленьких значений разрешена денормализация) изображён с переменным масштабом.

Рис. 4. Пример множества чисел, представимых в формате с плавающей запятой, переменный масштаб
В данном случае шаг меняется от 0,00001 до 100. Если не считать денормализованных значений, то постоянно количество значащих цифр – в примере их всегда три, по размеру мантиссы.
В общем-то, в этих картинках – вся суть, остальное – просто следствия – примеры применения этой модели, демонстрирующие проявляющиеся на практике отличия от «математических» чисел.
Любое действительное число можно абсолютно точно представить в виде бесконечной десятичной (или двоичной, или любой другой) дроби. Проблема в том, что у нас дробь – конечная.
Допустим, мы умеем точно записать некоторое число в виде бесконечной дроби (есть алгоритм, позволяющий каждый раз получить следующую цифру; простейший пример – периодическая дробь). Например:
1/3 = 0,33333333… 2/3 = 0,66666666… |
Для получения конечной дроби – округляем до нужного количества знаков. Для начала – просто отбросим лишнее:
1/3 = 0,3333 2/3 = 0,6666 |
В первом случае отброшено 0,000033333…, во втором 0,000066666… Очевидно, что величина всех отброшенной части меньше, чем единица младшего из оставленных разрядов – и это верно независимо от содержимого отброшенной части. То есть, единица младшего разряда – максимальная погрешность перевода при таком способе округления.
Более интеллектуальный способ округления предполагает анализ отбрасываемой части:
1/3 = 0,3333 2/3 = 0,6667 |
В первом случае отброшено 0,000033333…, во втором добавлено 0,000033333… (этот факт менее очевиден, проверяется вычитанием). Это называется «округление к ближайшему» – если вспомнить точки на прямой, то в качестве округлённого значения берётся ближайшая точка. При округлении к ближайшему погрешность округления будет не больше половины единицы младшего разряда.
Теперь, возьмём длинный-длинный ряд чисел, сложим их, и округлим результат. А теперь наоборот – сначала округлим каждое число, а затем сложим. Несложно привести примеры, когда результаты будут разные:
0,7 + 0,6 = 1,3 --> 1 0,7 + 0,6 --> 1 + 1 = 2 |
Но, так как по условию ряд не просто длинный, а «длинный-длинный», можно предположить, что округляемые «хвосты» распределены приблизительно равномерно. То есть, чисел вида xxx,2 столько же, сколько xxx,8, и на каждое округление вниз найдется примерно столько же округлений вверх. Проблема только с числами xxx,5 – для такого числа нет пары, оно всегда округляется вверх, значит результат будет смещённым – не просто неточным, а стабильно выше.
| ПРИМЕЧАНИЕ Если вы ещё помните теор.вер., то речь о том, что математическое ожидание суммы округлённых числе не совпадает с округлённой суммой – это и называется смещением. |
Для решения этой проблемы, числа вида xxx,5 нужно округлять иногда вниз, а иногда вверх – так, чтобы получилось примерно поровну. Распространённый вариант – округление таких чисел к ближайшему чётному (все остальные числа – как обычно, к ближайшему):
4,5 --> 4 5,5 --> 6 |
В предположении, что чётные/нечётные будут с равной частотой попадаться снизу и сверху, это даёт несмещённую сумму и погрешность округления не более половины младшего разряда.
| ПРИМЕЧАНИЕ Если округляется не один знак, а несколько, значимость этой поправки снижается – она работает только в ситуации «ровно пополам», если есть перевес вверх или вниз, округление идёт по общим правилам. Понятно, что чем больше знаков отбрасывается, тем меньше вероятность встретить «ровно половину» – xxx,5 встречается примерно в 1/10-й случаев, а xxx,500 примерно в 1/1000-й. |
Ну и, помимо прочего, нельзя забывать, что «единица младшего разряда» это «расстояние до соседнего», а оно у чисел с плавающей запятой меняется.
Уж как в правую дорожку ехать — убиту быть, Ай прямоезжую дорожку ехать — жонату быть, Во леву руку-де ехать — да всё богату быть. Три поездки Ильи Муромца
Возьмём два красивых числа 1/3 и 1/7, представим их в виде десятичных дробей с четырьмя знаками после запятой (выполним корректное округление), вычтем одно представление из другого.
1/3 --> 0,3333 1/7 --> 0,1429 1/3 – 1/7 --> 0,3333 – 0,1429 = 0,1904 |
А теперь наоборот – сначала вычтем, а потом переведём в десятичную дробь.
1/3 – 1/7 = 7/21 – 3/21 = 4/21 --> 0,1905 |
Результаты получились разные. В данном случае погрешность преобразования «обыкновенная дробь» --> «десятичная дробь с четырьмя знаками после запятой» не превышает половины младшего разряда, но числа подобраны так, что при вычитании погрешности складываются и суммарная погрешность оказывается больше.
Пример, конечно, наивный, но соль не в вычитании, а в общем принципе – математически-одинаковые числа, полученные двумя разными способами, на практике могут оказаться разными – из-за различий в последовательности выполнения округлений.
Мораль #1: если два числа нужно сравнить на равенство, рассчитывать на точное равенство наивно. Об этом «знают все», но, тем не менее, обычно понимают не совсем правильно, так что этому вопросу посвящён раздел «[Следствия] Сравнение».
Мораль #2: раз числа отличаются, скорее всего, одно из них точнее. Значит, выбирая последовательность действий, можно оптимизировать результат по точности. Наглядная иллюстрация приведена в следующем разделе.
Переменный шаг имеет следующий побочный эффект:
6780 + 3,14 = 6783,14 = (округляем до ближайшего с учётом текущей точности – 10) = 6780 |
Несложная программка:
#include <stdio.h>
int main()
{
float f = 100000000.0f; // 100 миллионов
printf("%f\n", f);
for (int i = 0; i < 1000; i++)
{
f += 1;
}
printf("%f\n", f);
f += 1000;
printf("%f\n", f);
}
|
.. воспроизводит его на практике. Результат работы:
100000000.00000 100000000.00000 100001000.00000 |
Секрет в том, что тип данных float [обычно] имеет точность 7-8 десятичных знаков (подробнее о том, почему так – см. ниже, в описании формата одинарной точности IEEE 754), для 100 миллионов восьмой знак это уже не единицы, а десятки. Поэтому прибавляем 1, получаем 100 000 001, округляем до восьми знаков, получаем обратно 100 миллионов. А если сразу прибавить 1000 – честно прибавляется.
Если в примере заменить float на double, фокус не пройдёт – точность double 15-16 десятичных знаков. Впрочем, несложно подобрать такое начальное значение, чтобы и у double всё было в порядке.
Мораль: складывать большие и маленькие числа нужно осторожно. Например, если нужно с большой точностью сложить много чисел, то начинать стоит с самых маленьких, и складывать не всё подряд, а группировать числа так, чтобы всё время суммировать значения приблизительно одного порядка – это как раз та ситуация, когда зависимость результата от пути видна очень явно.
((((12 + 0,42) + 0,43) + 0,45) + 0,48) = 12 – перебил всех по одному 12 + (0,42 + 0,43 + 0,45 + 0,48) = 14 – а когда навалились все сразу... |
Наглядное проявление принципа «вместе мы – сила» :)
| ПРИМЕЧАНИЕ То есть, с математической точки зрения, операция сложения чисел с плавающей запятой не ассоциативна: (a + b) + c != a + (b + c). Числа с фиксированной запятой этого недостатка лишены – как раз со сложением у них всё в порядке. |
Вычитание маленького из большого работает так же, как и сложение – при определённых условиях, маленькое можно просто отбросить.
6780 – 3,14 = 6776,86 = (округляем до ближайшего с учётом текущей точности – 10) = 6780 |
Это понятно. Но есть и вторая опасность – вычитание большого из большого. Казалось бы,
6781,35 – 6774,22 = 7,13 – получили три знака, что и требовалось, даже округлять не надо. |
Но дело в том, что округление произойдёт до вычитания:
6781,35 – 6774,22 = 6780 – 6770 = 10,0 |
Проблема в том, что в результате мы получаем маленькое число с маленькой точностью. Если в исходных числах после округления было три верных знака, то у результата – только один. Если мы на него что-нибудь умножаем-делим, ошибка будет распространяться и расти дальше.
Например, поставив в нескольких местах вызовы вот такой несложной функции:
double corrupt(double d)
{
return (d – d * 0.9999) * 10000;
}
|
можно увеличить погрешность до любого нужного значения.
Должно же у чисел с плавающей запятой быть что-то хорошее! Так вот, умножение – как раз хорошее.
Умножением в столбик легко проверить, что если умножаются два n-разрядных числа, результат получается 2n-разрядным (или на 1 разряд меньше). Но это верно, если исходные числа – точные (например, целые). Если же число не целое, а получено из какой-то функции (синус, логарифм) или переводом из другой системы счисления, оно никогда не будет точным, в лучшем случае оно получено с точностью до половины младшего разряда.
Пусть у нас есть числа 345 и 47,8, и точность у них – половина младшего разряда. Перемножим:
345 * 47,8 = 16491,0 |
Как и ожидалось, получили шесть знаков. Теперь перемножим истинные значения:
(345 + 0,5) * (47,8 + 0,05) = 345 * 47,8 + (0,5 * 47,8 + 345 * 0,05 + 0,5 * 0,05) = 16491,0 + 41,4525 |
Из этих шести знаков, на правду похожи только первые три, и в последнем из этих трёх ошибка на единицу. Результат общий: если у множителей точность n знаков, точность произведения тоже примерно n знаков. Значит от него имеет смысл оставить только старшие n разрядов, а все младшие – отбросить.
Именно так и работают числа с плавающей запятой! Старшие n разрядов укладываются в n-разрядную мантиссу, младшие – округляются:
345 * 47,8 = 3,45*102 * 4,78*101 = 1,6491 * 104 = (округляем до трёх знаков) = 1,65 * 104 |
Для начала, ещё раз повторим вывод про разные пути и разные результаты:
… математически-одинаковые числа, полученные двумя разными способами, на практике могут оказаться разными – из-за различий в последовательности выполнения округлений.
Во-первых, нужно чётко понимать причину: различные округления, вызванные разной последовательностью операций. Никакой магии, случайного шума, вероятностей или неопределённости. Числа, полученные одним способом, гарантировано будут одинаковыми: в одинаковых условиях детерминированный алгоритм (сложение, умножение и т.п.) возвращает одинаковые результаты. Если во время вычислений округлений не было (например, работаем с небольшими целыми числами), опять же, результат будет точным. В случаях вида:
double x = 2.0/3.0;
double y = x; // никаких округлений, просто присваивание
if (x == y)
{
// будет так
}
else
{
// смените процессор или компилятор, кто-то из них врёт
}
|
тоже никаких сюрпризов быть не должно.
Во-вторых, что делать, если числа всё-таки получены разными путями. Обычно поступают примерно так:
if (abs(x – y) < my_epsilon) // my_epsilon = 0,000001
{
// Условно равны
}
else
{
// Не равны
}
|
Это работает, если вы достаточно хорошо представляете масштаб x и y, и можете разумно выбрать константу для сравнения. Например, если значения x и y порядка 10-19, то эпсилон равный 0,000001, очевидно, не имеет смысла. Но и слишком маленький эпсилон тоже не хорош, из-за описанных выше особенностей вычитания он просто не даст никакого эффекта. Истина – в гармонии с реальными данными.
Более продвинутый вариант не нуждается в поиске гармонии, так как оценивает относительную, а не абсолютную погрешность:
if (abs(x – y) < 0,00001 * max(abs(x), abs(y)))
{
// Условно равны
}
else
{
// Не равны
}
|
Такая проверка выполняется в несколько раз медленнее, зато одинаково хорошо справляется с числами из любых диапазонов.
Теперь заметим, что если мы сравниваем числа, лежащие около 1.0, относительная погрешность равна абсолютной. Минимальная абсолютная погрешность в этом случае будет равна значению младшего разряда мантиссы числа 1.0 (всем понятно, что у разных чисел значения младших разрядов мантиссы могут отличаться?). За допустимую абсолютную погрешность можно взять минимальную, умноженную на какое-нибудь взятое с потолка число… И использовать результат как допустимую относительную погрешность в общем случае.
Для double и float в файле float.h определены константы DBL_EPSILON и FLT_EPSILON, равные соответствующим минимальным погрешностям (обычно эти константы описываются немного другими словами, как-нибудь самостоятельно разберитесь, почему это одно и то же). Использование может выглядеть так:
if (abs(x – y) < DBL_EPSILOB * 1000 * max(abs(x), abs(y)))
{
// Условно равны
}
else
{
// Не равны
}
|
| ПРИМЕЧАНИЕ Большое спасибо McSeem2у и Eropу за объяснения, дополнения и направления на путь истинный. |
Числа с плавающей запятой предполагают разделение труда – за диапазон отвечает показатель степени, за точность – мантисса. В результате при любом диапазоне можно использовать всю мантиссу – все n знаков.
3,844 * 108 (расстояние до Луны в метрах) 1,2 * 10-2 (средний размер рыжего таракана, в метрах) |
могут быть с успехом записаны в одном и том же формате, отводящем 4 разряда под мантиссу и 1 под показатель степени – их точность не превышает 4 знака, а значение по модулю не слишком велико.
| ПРИМЕЧАНИЕ Измерение точности в знаках – приближение. Кричащий пример: одноразрядные числа 1 и 9 получены с погрешностью не более половины младшего (и единственного) разряда. Но, если переводить в проценты, в первом случае погрешность может достигать 50%, а во втором – не более 5,6% – в 9 раз точнее. Обобщая: пока абсолютная погрешность постоянна, чем число больше, тем оно точнее (в процентах). Разброс по точности между 1000 и 9999 будет примерно в 10 раз – и это число не случайно совпадает с основанием системы счисления. С этой точки зрения двоичная система оптимальна – в ней минимальна разница между максимальным и минимальным значением одной длины. Чем больше основание – тем хуже. Ещё хуже – у денормализованных чисел – при денормализации происходит «деградация точности». В этом аспекте они похожи на числа с фиксированной запятой (а у тех, соответственно, с «точностью в процентах» тоже всё плохо). |
Если вернуться к картинкам с точками на прямой (рисунки 2, 3, 4), то числа с фиксированной запятой это своеобразная «уравниловка»: для любого значения шаг одинаков. Чтобы в одном формате с фиксированной запятой представить и самое маленькое (по модулю) и самое большое число из представимых в формате с плавающей запятой, нужно гораздо больше разрядов (в примере 10: 5 перед запятой и 5 после – против 4-х разрядов числа с плавающей запятой).
Больше разрядов сделать можно (хотя, смотря на сколько: всего 2 десятичных разряда на показатель степени, и для фиксированной запятой нужно 100 разрядов), но это очень не экономно – и по памяти и по скорости обработки. Тем более, что практически никогда эти разряды не будут использоваться полностью – числа, которым нужна точность до 100-го разряда на практике не встречаются.
Число с плавающей запятой предлагает компромисс: можно работать с очень большими, можно с очень маленькими, можно – со средними. Со всеми – одинаково удобно, с одинаковой точностью, в одном и том же формате – масштабный коэффициент вводится незаметно. И – не слишком дорого.
Если же вам всё-таки нужно к очень большому прибавить очень маленькое – да, у вас проблемы. Но вы действительно уверены, что «очень большое» число известно с достаточной точностью и прибавлять к нему маленькое – имеет смысл? Если да, и ни один из форматов нужной точности не обеспечивает – видимо нужно разрабатывать формат самостоятельно и реализовывать его – программно или аппаратно. Но такие случаи всё-таки довольно редки.
| ПРИМЕЧАНИЕ Тут можно было бы вспомнить о криптографии – RSA использует огромные числа. Но, во-первых, там числа целые, во-вторых, на них никаких форматов не напасёшься – рекомендации на размер ключей растут с ростом быстродействия компьютеров. |
Все люди делятся на 10 типов: те, кто понимают двоичную систему счисления и те, кто нет.
Всё то же самое в преломлении двоичной системы счисления и приложении к конкретным компьютерам приобретает новые красочные оттенки.
Переводить целые числа из двоичной системы в десятичную и обратно умеют почти все. С дробями, в общем, не сильно сложнее. Для начала нужно осознать, чему равна дробь, записанная в позиционной системе счисления.
На примере десятичных:
0,357 = 3/10 + 5/100 + 7/1000 = 3*10-1 + 5*10-2 + 7*10-3 |
Обобщаем до системы счисления с основанием q:
0,a1a2…an = a1q-1+ a2q-2 + .. + anq-n |
Распространяем на двоичный случай:
0,1100101 = 1*2-1 + 1*2-2 + 0*2-3 + 0*2-4 + 1*2-5 + 0*2-6 + 1*2-7 = 1/2 + 1/4 + 1/32 + 1/128 = 0,5 + 0,25 + 0,03125 + 0,0078125 = 0,7890625 |
Именно так двоичные дроби переводятся в десятичные (точнее, именно так они переводятся людьми на бумажке, компьютеру проще действовать иначе). Алгоритм основан на том, что мы умеем выполнять арифметические действия в целевой системе счисления – в результате значение дроби получается простым выписыванием многочлена.
Рассмотрим обратную ситуацию. Пусть F – число от 0 до 1 (включая ноль, исключая 1), записанное в каком-то виде – не важно в каком, важно чтобы мы умели работать с такими числами. На выходе нужно получить дробь, записанную в позиционной системе счисления по основанию q. Запишем что-то типа уравнения:
0,x1x2x3…xm… = F |
Справа – исходная дробь, слева – результат преобразования в виде потенциально бесконечной строки неизвестных.
| ПРИМЕЧАНИЕ Разрядность зависит от требований к точности преобразования, от размера разрядной сетки. Возможно ли точное представление F в целевой системе счисления мы заранее не знаем (например, 1/3 в десятичной), сколько разрядов для этого потребуется тоже не знаем. |
При умножении обеих частей на q, получим:
x1,x2x3…xm… = F*q |
Так как мы умеем работать с числом F, мы можем вычислить F*q, а так как исходно F меньше единицы, F*q окажется меньше q. Поскольку числа равны, соответственно равны и их целые и дробные части:
x1 = [F*q]
0,x2x3…xm… = {F * q}
|
В результате мы получили значение x1, а вычисление оставшейся части дроби свели к исходной задаче.
Пример: представим 1/3 в виде 5-и разрядной двоичной дроби.
По правилу, x5 должен быть равен 0. Но, т.к. это последний из рассматриваемых битов (из соображений разрядности или точности – не важно), здесь разумно применить округление. В результате x5 = 1. Общий результат – 0,01011
Второй пример – десятичное 0,1 в двоичную дробь.
В результате 0,1d = 0,0(0011)b
| ПРИМЕЧАНИЕ Обратите внимание! Красивое круглое десятичное число 0,1 в двоичном виде представимо только как бесконечная периодическая дробь. |
Естественно, в памяти компьютера двоичное число с плавающей запятой представлено набором битов. Существует много (см. http://home.earthlink.net/~mrob/pub/math/floatformats.htm) стандартов на форматы представления, но почти все они построены по одному шаблону:
Общая схема изображена на рисунке 5.
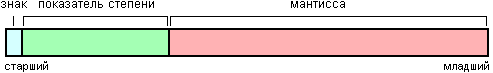
Рис. 5. Число с плавающей запятой в памяти. Картинка скопирована из http://en.wikipedia.org/wiki/IEEE_754-1985 и немного переделана.
Знак числа вынесен в отдельное поле, а мантисса считается всегда положительной. Про показатель степени я напишу чуть ниже.
Как вы помните, условием нормализации является 1 <= M < q. Для двоичной системы это означает 1 <= M < 2. То есть, если число нормализовано, целая часть M всегда будет равна 1 (ноль не подходит, а других вариантов нет). Значит, можно сэкономить на этом бите – не хранить, а только подразумевать его наличие.
Этот нехитрый приём используется в нескольких распространённых стандартах. Обычно это называется hidden bit.
Небольшая проблема возникает при попытке представить в таком виде число 0… Проблема решаемая – ноль рассматривается как отдельный случай.
Показатель степени – целое число, он может быть как положительным, так и отрицательным. Видимо, для того, чтобы не возиться с отрицательными числами, обычно он хранится в виде беззнакового целого со смещением. А для того чтобы получить реальное значение показателя степени, нужно вычесть из записанного значения некоторую константу.
1,72 * 102 = 1,72 * 1052-50 = 1,72 * 10502-500 1,72 * 10-2 = 1,72 * 1048-50 = 1,72 * 10498-500 |
Понятно, что это равносильно введению соответствующего масштабного коэффициента, несложно модифицировать алгоритмы операций над числами так, чтобы они его учитывали.
Ниже описано семь различных форматов… Хотя, казалось бы, вполне достаточно одного – выбрать какой-нибудь с хорошим запасом точности и диапазона, и использовать везде. Например, такой: http://en.wikipedia.org/wiki/Quadruple_precision – хватит всем.
Два фактора, способствуют разнообразию форматов: технические ограничения и экономия. Причём обычно они работают вместе. Например, если видеокарте нужно обработать 109 чисел в секунду, ей глубоко небезразлично, каков размер этих чисел – скорость операций сложения и умножения зависит от количества разрядов, количество транзисторов, уходящих на один сумматор/умножитель – тоже зависит. От количества транзисторов зависит размер кристалла, его цена, требуемое питание и охлаждение.
Дальше, все эти числа нужно передавать между центральным процессором и видеокартой, и вопрос, влезают ли они в пропускную способность канала тоже не праздный. Чем меньше разрядов, тем, очевидно, легче влезают.
Если мы теперь определим верхнюю границу стоимости разрабатываемого устройства и учтём пропускную способность шины, то, скорее всего, окажется, что 128 бит – многовато. Да и вообще, в данном случае понятно, что чем меньше – тем лучше – до тех пор, пока качество остаётся приемлемым. А выгоднее всего остановиться примерно на границе приемлемого качества: пользователь всё равно разницу не заметит, а сэкономить можно очень прилично.
Но видеокарта это устройство, за которое пользователь готов платить, и даже покупать ради неё системную плату с более быстрой шиной. Чем меньше готов платить пользователь, тем важнее экономия. И при переходе от PC (в классическом применении – когда мощность практически не считается) к встроенным системам могут использоваться достаточно экзотичные варианты, которые, впрочем, выходят за рамки статьи.
Наиболее распространённый в данный момент стандарт, реализован во всех x86-совместимых процессорах, в PowerPC, во многих микроконтроллерах; описывает три вида чисел с плавающей запятой. Принят в 1985-м году, сейчас находится в процессе ревизии.
Стандарт описывает:
Мы рассмотрим только первые два пункта. Кроме того, три вида чисел отличаются друг от друга, практически, только разрядностью мантиссы и показателя степени, особые случаи у всех одинаковы, поэтому рассмотрены отдельно.
| Знак | Показатель степени | Мантисса | Что это, доктор? |
| 0 | 00..00 | 00..00 | Положительный ноль |
| 1 | 00..00 | 00..00 | Отрицательный ноль |
| x | 00..00 | Не ноль | Очень маленькое число. Показатель степени принимается минимальным для формата (то есть, таким же, как для случая, когда в поле показатель степени записано 00..01), мантисса не нормализована (значение скрытого бита – 0). |
| x | 00..00 < p < 11..11 | Любая | Обычное число. Для получения реального значения показателя степени, из p нужно вычесть 01..11 |
| 0 | 11..11 | 00..00 | Плюс бесконечность |
| 1 | 11..11 | 00..00 | Минус бесконечность |
| x | 11..11 | Не ноль | NaN, Not-a-number – не число |
Что интересного в ней можно заметить:
Знак – 1 бит, показатель степени – 8 бит (смещение 127), мантисса – 23 бита + 1 скрытый. Всего 32 бита.
В двоичных знаках понятно – раз мантисса 24 бита, значит и точность 24 двоичных знака. Разберёмся с десятичными.
Поскольку для точности «в знаках» масштаб не имеет значения, умножим мантиссу на 224. Показатель степени на точность не влияет, так что его можно оставить как есть. Получившееся целое число мантисса представляет точно. Для его представления в десятичном виде нужно:
log10224 = 24 * log102 = 7,2 десятичных знака |
Это значит, что погрешность двоичного представления числа не превосходит половины седьмого десятичного знака, даже чуть меньше.
Для примера, представим в этом формате число 1234,5.
Ещё несколько характерных примеров приведено в таблице 2.
| Знак | Показатель степени | Мантисса | Значение | |
|---|---|---|---|---|
| 1234,5 | 0 | 1000 1001 | 001 1010 0101 0000 0000 0000 | 1234,5 |
| Ноль | 0 | 0000 0000 | 000 0000 0000 0000 0000 0000 | 0 |
| Один | 0 | 0111 1111 | 000 0000 0000 0000 0000 0000 | 1 |
| Наименьшее ненормализованное | 0 | 0000 0000 | 000 0000 0000 0000 0001 0000 | 1,4*10-45 |
| Наибольшее ненормализованное | 0 | 0000 0000 | 111 1111 1111 1111 1111 1111 | 1,8*10-38 |
| Наименьшее нормализованное | 0 | 0000 0001 | 000 0000 0000 0000 0000 0000 | 1,8*10-38 |
| Наибольшее нормализованное | 0 | 1111 1110 | 111 1111 1111 1111 1111 1111 | 3,4*1038 |
| Бесконечность | 0 | 1111 1111 | 000 0000 0000 0000 0000 0000 |
В языках C/C++ числам одинарной точности обычно соответствует тип данных float.
| ПРИМЕЧАНИЕ Конечно, стандарт C/C++ не привязан к стандартам на числа с плавающей запятой и не регламентирует этот момент, иначе было бы невозможно писать на C для платформ, не поддерживающих IEEE 754. Тем не менее, для большинства платформ и компиляторов… |
Зная формат, несложно написать соответствующую структуру:
union ParsedFloat
{
float v; // значениеstruct
{
unsignedint m : 23; // мантиссаunsignedint e : 8; // показатель степениunsignedint s : 1; // знак
} f;
};
|
| ПРЕДУПРЕЖДЕНИЕ Скорее всего, тут важен порядок байт, и для процессоров, работающих с числами в формате big endian, структура будет выглядеть иначе. |
И на собственном опыте убедиться в правильности/ошибочности описанной выше теории (или правильности/ошибочности её интерпретации). Например, так:
#include <stdio.h>
union ParsedFloat
{
float v; // значениеstruct
{
unsignedint m : 23; // мантиссаunsignedint e : 8; // показатель степениunsignedint s : 1; // знак
} f;
};
int main()
{
ParsedFloat pf;
pf.f.m = 0x1a5000; // 001 1010 0101 0000 0000 0000
pf.f.e = 0x89; // 1000 1001
pf.f.s = 0; // 0
printf("%f", pf.v);
}
|
Знак – 1 бит, показатель степени – 11 бит (смещение 1023), мантисса – 52 бита + 1 скрытый. Всего 64 бита.
Поскольку никаких существенных отличий от чисел одинарной точности нет, а примеры 64-х битных чисел выглядят уже слишком громоздко, обойдёмся без примеров.
С теми же оговорками что и про float, в C/C++ числам двойной точности соответствует тип double. Структура выглядит так:
union ParsedDouble
{
double v; // значениеstruct
{
unsignedint m0; // младшие биты мантиссыunsignedint m1 : 20; // старшие биты мантиссыunsignedint e : 11; // показатель степениunsignedint s : 1; // знак
} d;
};
|
Стандарт не оговаривает точные значения размеров – только нижние границы, более того, даже не оговаривается, имеет ли мантисса скрытый бит; всё это остаётся на совести реализации. На практике встречается следующий вариант (реализован во всех x86-совместимых процессорах):
Знак – 1 бит, показатель степени – 15 бит (по стандарту – не меньше 15-ти), мантисса – 64 бита (по стандарту – не меньше 64-х), скрытого бита нет. Всего 80 бит.
| ПРИМЕЧАНИЕ Во времена Intel 486, процессор работал с числами с плавающей запятой именно в этом формате – это формат регистров FPU. Числа одинарной и двойной точности преобразовывались в расширенный формат «на лету», до начала операции. С появлением SSE 2,3,4 ситуация изменилась, но эти подробности выходят за рамки статьи. |
В С/C++ числам расширенной точности соответствует (со стандартными оговорками) тип long double… Вот только он не поддерживается в Microsoft Visual C++ :) Точнее, VC игнорирует long и считает этот тип синонимом обычного double.
В GCC же следующая конструкция вполне работоспособна:
union ParsedExtended
{
longdouble v; // значениеstruct
{
unsignedint m0; // младшие биты мантиссыunsignedint m1; // старшие биты мантиссыunsignedint e : 15; // показатель степениunsignedint s : 1; // знак
} d;
};
|
Числа в следующих форматах сложно встретить в повседневной жизни, но знать о них полезно – чтобы не зацикливаться на IEEE 754 да и вообще для расширения сознания.
Коротенький 16-и битный формат, построенный по аналогии с IEEE 754, возможно будет включен в IEEE 754 после ревизии.
Знак – 1 бит, показатель степени – 5 бит (смещение 15), мантисса – 10 бит + 1 скрытый. Всего 16 бит.
Используется в OpenGL и графических процессорах (в частности – для представления яркости пикселя). Немного более подробно можно почитать по ссылкам:
8 бит – достаточно. Особенно, если знать, что c ними делать :)
Знак – 1 бит, показатель степени – 4 бита (смещение -2; ещё раз, прописью: минус два), мантисса – 3 бита + 1 скрытый. Всего 8 бит.
Чтобы понять, как это работает, вернёмся чуть назад, вспомним, что такое смещение показателя степени. В формате IEEE 754 значение показателя степени может быть как положительным, так и отрицательным, но хранится в виде «реальное значение + смещение», где смещение подобрано так, что его сумма с реальным значением всегда положительна.
Смещение -2 означает, что показатель степени хранится в виде «реальное значение – 2». Далее, если следовать правилам IEEE 754, то:
В таблице 3 приведено несколько примеров.
| Биты | Значения с поправками | Результат | Комментарий |
|---|---|---|---|
| 0 0000 000 | P = 3; M = 0,000 | 0 | |
| 0 0000 001 | P = 3; M = 0,001 | 1 | Минимальное ненормализованное |
| 0 0000 010 | P = 3; M = 0,010 | 2 | |
| 0 0000 111 | P = 3; M = 0,111 | 7 | Максимальное ненормализованное |
| 0 0001 000 | P = 3; M = 1,000 | 8 | Минимальное нормализованное |
| 0 0001 111 | P = 3; M = 1,111 | 15 | |
| 0 0010 000 | P = 4; M = 1,000 | 16 | До сих пор значения чисел шли через 1, и, кстати, совпадали со значением обычного 8-и битного целого. |
| 0 0010 001 | P = 4; M = 1,001 | 18 | Первое отличие |
| 0 1010 001 | P = 12; M = 1,001 | 9*29 = 4 608 | (*) |
| 0 1010 010 | P = 12; M = 1,010 | 10*29 = 5 120 | (*) |
| 0 1110 111 | P = 16; M = 1,111 | 15*213 = 122 880 | Максимальное значение с NaN-ами и бесконечностями |
| 0 1111 111 | P = 17; M = 1,111 | 15*214 = 245 760 | Максимальное значение без NaN-ов и бесконечностей |
Как видно, при некотором желании, в один байт помещаются числа от -245760 до +245760. Естественно, не бесплатно, а за счёт потери точности. Обратите внимание на строчки таблицы, отмеченные звёздочкой. Это два соседних значения.
Полезные ссылки:
IBM System/360 – семейство мэйнфреймов фирмы IBM, их выпуск начался в 1964-м году – за 20 лет до принятия стандарта IEEE 754 – и угадать заранее не получилось. Начиная с 1988-го года мэйнфреймы-преемники IBM S/360 поддерживают оба стандарта на форматы чисел с плавающей запятой.
Стандарт IBM имеет три существенных отличия от IEEE 754:
Стандарт описывает два формата – 32 и 64 бита, но отличаются они только размером мантиссы. В цифрах:
Представим в формате single precision уже знакомое нам число 1234,5:
Полезные ссылки:
Она на подходе! Обсуждение идет начиная с 2000-го. Из открытий чудных, которые нам готовят:
Ссылки:
Квест пройден! Вы получили +100 к опыту и +200 к умению ковыряться в битах :)
Но… Вы думаете, что теперь вы знаете про числа с плавающей запятой всё? Ну, или хотя бы – много? Огорчу вас – тема неожиданно огромна.
В статье весьма поверхностно рассмотрены операции над числами и точность, вообще ничего не сказано про исключения, про особые числа, про отличия в реализациях форматов на разных платформах, про скорость выполнения, про всякие экзотические форматы… Дальше начинается смежная тема – приблизительное вычисление невычислимых функций – возможны оптимизации по точности, скорости, памяти, всякие интересные численные методы. Дальше, наверное, мат.статистика :)
И, если глубины знаний манят вас – все дороги открыты. Сначала по ссылкам, потом по ссылкам из ссылок, потом получаете богатый практический опыт (хотя это можно и первым и вторым пунктом), потом – пишите монографию (очень систематизирует знания) ну и поучаствуйте в разработке следующей версии стандарта – тоже полезно, в рабочей группе будет много неглупых людей с уникальным опытом.
Работы на ближайшие года два минимум.
Но, для программиста, который не стремиться ворочать битами, хотя и не чурается этого, изложено достаточно – примерно столько, сколько знаю я :) И совершенствовать свои познания в этой области я в ближайшем будущем не собираюсь…
2.1. Стандарты (в преддверии ревизии их выложили, а на http://ieee.org всё ещё пытаются продавать):
2.2. Немножко вики
2.3. Разное
 Оценка 735
[+1/-0] Оценка 735
[+1/-0]
  Оценить Оценить       
|