Сообщение Re[2]: Подскажите либу для сплайна от 27.09.2023 15:11
Изменено 27.09.2023 17:25 Chorkov
Re[2]: Подскажите либу для сплайна
Здравствуйте, kov_serg, Вы писали:
_>Здравствуйте, Serpuh, Вы писали:
S>>Цель — получить ур-е плоскости в пространстве перпендкулярное сплайну в заданной точке. Или упрошенный вариант — ур-е перпедикулярной прямой для 2d сплайна xy в заданной точке. Среда разработки Линукс.
_>
_>Это ж элементарно:
_>Rxyz=F(t) — сплайн Rx=Fx(t), Ry=Fy(t), Rz=Fz(t)
_>t=[0..1]
_>Fdot(t) — производная от F -- Fdot(t) = (F(t+dt)-F(t)) / dt при dt->0
_>( r — F(t) , Fdot(t) )=0 -- уравнение плоскости перпендикулярной сплайну, r точка плоскости
_>или если расписать
_>(x-Fx(t))*Fdotx(t) + (y-Fy(t))*Fdoty(t) + (z-Fz(t))*Fdotz(t)) = 0
_>F — зависит от типа сплайна, но обычно это просто полином или много полиномов на разных кусках интервала от 0..1
_>Для 2d тоже самое только без z координаты
Это элементарно, если у есть физический параметр (типа, пройденной дистанции) по которому кривая праметризуется "естественным" образом.
Если есть только точки и они неоднородно распределены в пространстве — то проблема.
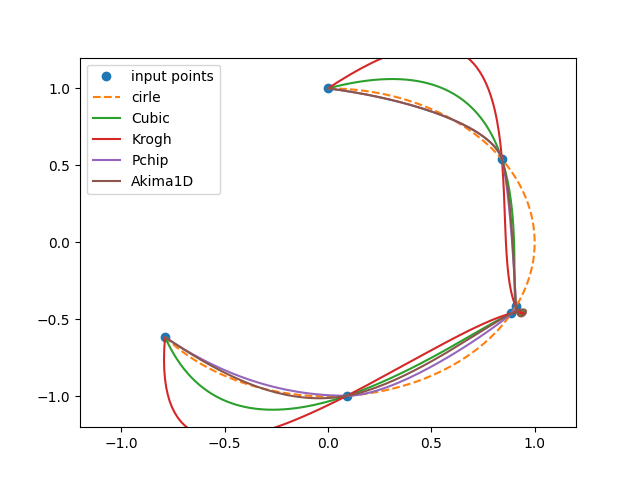
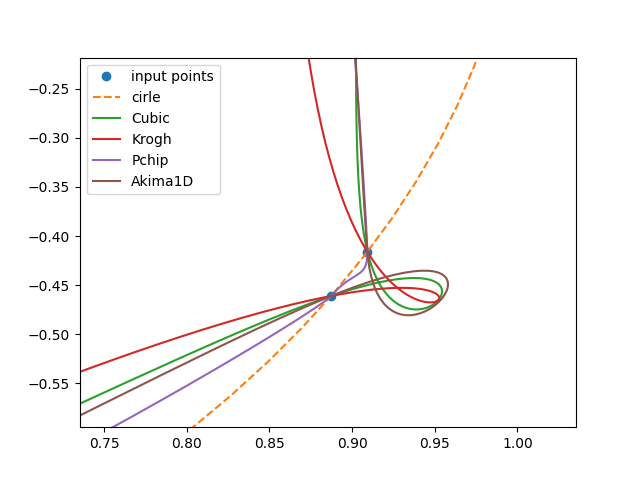
Берем точки на окружности, но распределенные неравномерно, (две рядом), и пытаемся применить ваш алгоритм:
_>Здравствуйте, Serpuh, Вы писали:
S>>Цель — получить ур-е плоскости в пространстве перпендкулярное сплайну в заданной точке. Или упрошенный вариант — ур-е перпедикулярной прямой для 2d сплайна xy в заданной точке. Среда разработки Линукс.
_>
_>Это ж элементарно:
_>Rxyz=F(t) — сплайн Rx=Fx(t), Ry=Fy(t), Rz=Fz(t)
_>t=[0..1]
_>Fdot(t) — производная от F -- Fdot(t) = (F(t+dt)-F(t)) / dt при dt->0
_>( r — F(t) , Fdot(t) )=0 -- уравнение плоскости перпендикулярной сплайну, r точка плоскости
_>или если расписать
_>(x-Fx(t))*Fdotx(t) + (y-Fy(t))*Fdoty(t) + (z-Fz(t))*Fdotz(t)) = 0
_>F — зависит от типа сплайна, но обычно это просто полином или много полиномов на разных кусках интервала от 0..1
_>Для 2d тоже самое только без z координаты
Это элементарно, если у есть физический параметр (типа, пройденной дистанции) по которому кривая праметризуется "естественным" образом.
Если есть только точки и они неоднородно распределены в пространстве — то проблема.
Берем точки на окружности, но распределенные неравномерно, (две рядом), и пытаемся применить ваш алгоритм:


| Исходник на питоне | |
| |
Re[2]: Подскажите либу для сплайна
Здравствуйте, kov_serg, Вы писали:
_>Здравствуйте, Serpuh, Вы писали:
S>>Цель — получить ур-е плоскости в пространстве перпендкулярное сплайну в заданной точке. Или упрошенный вариант — ур-е перпедикулярной прямой для 2d сплайна xy в заданной точке. Среда разработки Линукс.
_>
_>Это ж элементарно:
_>Rxyz=F(t) — сплайн Rx=Fx(t), Ry=Fy(t), Rz=Fz(t)
_>t=[0..1]
_>Fdot(t) — производная от F -- Fdot(t) = (F(t+dt)-F(t)) / dt при dt->0
_>( r — F(t) , Fdot(t) )=0 -- уравнение плоскости перпендикулярной сплайну, r точка плоскости
_>или если расписать
_>(x-Fx(t))*Fdotx(t) + (y-Fy(t))*Fdoty(t) + (z-Fz(t))*Fdotz(t)) = 0
_>F — зависит от типа сплайна, но обычно это просто полином или много полиномов на разных кусках интервала от 0..1
_>Для 2d тоже самое только без z координаты
Это элементарно, если есть физический параметр (типа, пройденной дистанции) по которому кривая праметризуется "естественным" образом.
Если есть только точки и они неоднородно распределены в пространстве — то проблема.
Берем точки на окружности, но распределенные неравномерно, (две рядом), и пытаемся применить ваш алгоритм:


_>Здравствуйте, Serpuh, Вы писали:
S>>Цель — получить ур-е плоскости в пространстве перпендкулярное сплайну в заданной точке. Или упрошенный вариант — ур-е перпедикулярной прямой для 2d сплайна xy в заданной точке. Среда разработки Линукс.
_>
_>Это ж элементарно:
_>Rxyz=F(t) — сплайн Rx=Fx(t), Ry=Fy(t), Rz=Fz(t)
_>t=[0..1]
_>Fdot(t) — производная от F -- Fdot(t) = (F(t+dt)-F(t)) / dt при dt->0
_>( r — F(t) , Fdot(t) )=0 -- уравнение плоскости перпендикулярной сплайну, r точка плоскости
_>или если расписать
_>(x-Fx(t))*Fdotx(t) + (y-Fy(t))*Fdoty(t) + (z-Fz(t))*Fdotz(t)) = 0
_>F — зависит от типа сплайна, но обычно это просто полином или много полиномов на разных кусках интервала от 0..1
_>Для 2d тоже самое только без z координаты
Это элементарно, если есть физический параметр (типа, пройденной дистанции) по которому кривая праметризуется "естественным" образом.
Если есть только точки и они неоднородно распределены в пространстве — то проблема.
Берем точки на окружности, но распределенные неравномерно, (две рядом), и пытаемся применить ваш алгоритм:


| Исходник на питоне | |
| |